| tree | functional term |
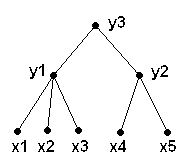
| y3 = f3( f1(x1, x2, x3), f1(x4, x5) ) |
Considered formal model appropriate for determining minimal period of memory variable existence. Offered an algotithm of minimization area of visibility and determination minimal period of existence of memory variable based on that model. This alorithm is intended for determination moment of allocation and deallocation memory variables.
Author : Petr Gladkikh, 2001, (e-mail: gladkikh@ssd.sscc.ru ).
Keywords : memory management; dynamic allocation; alghorithm; programming;
This paper is written because the author was faced with problem of automatical allocation and destroying of dynamically allocated variables. The sated questions are:
More general goal is to develop programming language with intensive utilizing of dynamic allocation technique. This technique is one of most promisable approaches allowing to optimize loading of all nodes of multiprocessor computer.
General aims of memory allocation is to minimize program memory requirements and to minimize data access time. These criteria often contradicts each other and developing of memory allocation techniques need to pay attention to both of them. But in this paper we consider only the first.
Significant distinction between approach offered in this paper from most approaches utilized in existing programming languages with automatical memory allocation (e.g. Java) is to analyse source code an then statically place allocation / deallocation procedures into program in the phase of compilation. Note that most of modern compilators performs optimization of variable existence period. But feature of stated approach is generalization of it on wider class of algorithms allowing to apply one to parallel programs.
Chapter 2 contains formal model of calculations allowing to formalize alghorithm to be introducesd. Chapter 3 states the problem and explains the goals of alghorithm. Chapter 4 describes the alghorithm. Chapter 5 applies aghorithm introduced in chapter 4 to certain kind of program which is conventional secuential program written in language of structured programming (e.g. Pascal or C).
Let's consider model of calculations based on functional programming viewpoint.
There is several ways to analise programs depending on abstraction level. Consider three levels of program representation starting from most general view and finishing with concrete program.
| tree | functional term |

| y3 = f3( f1(x1, x2, x3), f1(x4, x5) ) |
Most detailed view of program is tracing particular program with sertain input values. But this level is inappropriate for developing common algorithms.
In this paper we will use the following model which is function tree model with following extensions:
So algorithm representation consists of set of operations, set of information output-input depencities which imposes execution order restrictions, and additional constraints on order of operation execution which also called "direct control".
Operation is named object (e.g. a1, a2, ...). It has set input parameters {xi} and set output parameters {yi}. We will draw it as follows:
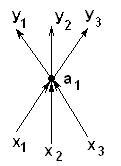
Let's define following notations:
In this paper we assume therms "operation", "function", "program procedure" to be equal.
One can determine two opposite approaches to dynamical allocation. First is to cteate all variables nessesary to program at it's start and destroy them all after it finished. Obviously this manner of allocating consumes too much memory and therefore is unapplicable. Second approach is to spy for all memory operations and allocate nessesary variables on the fly. In this case we should check for all memory operations in order to have opportunity to allocate variable that not exists yet. So such behavior occupies CPU time for inefficient work and reduces program performance. Another lack of this approach is automatical garbage collection expences which also conusumes CPU time.
At the same time both concidered approaches has it's own benefits. In first case we obtain simple program structure and efficient CPU utilisation. In the latter case we have minimal period of existence of allocated but not used variable.
Analisys of both cases may result to following idea: use source code analisys and theh statically distibute allocation/deallocation routines among program. This approach benefits in more eficient memory and CPU utilization rather than both initial techniques. The lack of this approach is nessesity to re-analyse whole program after one changes. So it reduces flexibility of compiled code.
Sertainli this approach can be modified to be similary to both initial techniques. Namely, we can utilize message passing technology to inform memory management facility about starting and completing of program operations and this facility can determine using alghorithm stated below if there nessesity of cerstin memory operations.
The conclusion idea is to allocate variable as later as it possible and destroy it as immediately after it no more nessesary. If we do so we obtain minimal period of variable existence and as a result we minimize memory utilization. Note that obtained period depends on order of program operations execution.
As we have noted earlier set of operations consisting the program can be interpreted as partly ordered set. Let's consider a variable v. This variable is changed and be readed by particular set of operations. Let's denote this set as M(v) and let the notation "A < B" to mean "operation A should be completed before operation B".
Let's consider set M(v). Variable v should be initialized before any operations in set M(v) started. We denote it as ini(v) < M(v). Similary variable v can be destroyed after (and not earlier than) all operations in set M(v) is completed. We denote it as follows M(v) < del(v).
It's better to free memory resource occupied by variable v before any operation in {p | p > M(v)} starts. Therefore, if no additional criteria specified, best area for placing destruction operator del(v) is
M(v) < del(v) < min {p | p > M(v)}
We can formulate it as
max M(v) < del(v) < sup M(v)
Similary we can say that
inf M(v) < ini(v) < min M(v)
Where min S defined as
{s | not exists p in S, p < s}.
and max S defined as
{s | not exists p in S, p > s}.
Note that these definitions are valid for sets consisting of one element.
In terms of partly ordered sets we need to find inf M(v), min M(v), maxM(v) and sup M(v). If we have obtained these subsets we can say that
inf M(v) < p < min M(v)
max M(v) < p < sup M(v)
Note that these speculations valid only if all nodes of considered subsets are "and" nodes. i.e. operation executes if all input variables have been calculated and operation always produces all it's output variables. At the same time real programs has predicative execution nodes, which can produce just a part of all it's output variables. This situation we consider later.
As it shown in previous chapter we need to formulate algorithm of finding min, max, inf and sup of given set of operations. This algorithm should be able to determine place for inserting ini and del operations. And here we are faced with following problem: in general case not all partly ordered sets have their inf and sup. And, at another hand, inf, sup, min or max may consists of more than one element. (In our case we could interest only in M(...) subsets.) Let's consider different cases of these issues.
Let's suppose that there is subset S of operations that haven't it's inf. It mean that min element (or elements) of S is in min Op. To avoid this situation we add pseudo operation "Start" which satisfy following condition: Start < Op. i.e. Start comparable with all operations in Op and should be performed before all of them. In practice we always can determine begin of program so this extension of algorithm not reduce generality of our speculations.
Similary we add operation "end" which satisfy condition Op < Fin. This operation is point of algorithm completion.
These two program extensions can be performed as follows:
for each r in Op
if not exists p : p < r, r in Op {
insert Start < r in Ord
}
for each r in Op
if not exists p : p > r, r in Op {
insert r < Fin in Ord
}
After these extensions each element in Op has it's inf and sup. And thus each subset in Op has it's inf and sup.
Below we consider only inserting of ini operator. Note that speculations about del operator may be conducted in similary way
Suppose that min M(v) = {m1, m2, ... mn} and inf M(v) = {l1, l2, ... lk}. If we determine these elements we can insert operator ini(v) as follows
(*)
This reordering can't change functional depencities. Let's proof it. Relation a < b in original algorithm replaces with relations a < ini(v) and ini(v) < b. From the latter two relations we obtain a < b. Also we need to note that stated conversion may add new order relations between set min M(v) and set inf M(v). But new order relations only reduces flexibility in choosing operation execution sequence not the algorithm correctness.
In fact after these conversionns operator ini(v) becomes synchronization point before starting any of M(v) opearions.
As it mentioned above if we have subsets L : L < M(v) there is relative freedom in choosing place for ini(v). But each choosen place for ini operator should satisfy the main restriction ini(v) < M(v).
Now we extend initial model to be more useful for application.
All abowe speculations have been applied to "flat" operation order restricitons. I.e. scheme of those restricitons supposed to be describing whole program model itself. But if we have any loops in ceratin program we need to introduce recursive program models. These models can contain structured nodes containing another program model.
Consider a loop in sequential program. Each exectution of loop body should be represented in functional term. It can be done by constructing recursive model where each loop body execution represented by recursive model.
One can try to expand recursive model by substituting structured nodes with respective definitions.
If structured node has non-recursive definition in finite number of steps we obtain model without recursive definition of those node and then one be able to analyse this model using methods described above. In other words loops with constant number of iterations after expansion can be handled as usual operations.
If we have structured nodes with recursive definitions i.e. model A refers model B, model B refers model C, ... and model Z refers model A. In this situation we can not completely expand given model.
Each execution of algorithm can lead different number of loop body executions. Indeed we have finite number of iterations because algorithm execution should be finite. In spite of this we can not predict within compilation process what number of iterations will be actually executed.
Whereas we should obtain appropriate estimates of of loop body scheme we can utilize two following approaches.
First approach allows us to obtain "good enough" M(v) set min and max estimates. To do this we should consider loop's scheme inf and sup as inf M(v) and sup M(v) respectively. It is obvious that this estimate is correct whereas estimate for structured operation is alsoe stimate for all subschemes it contains.
If we want to obtain more accurate estimates (e.g. in case of long loop body). We can expand first subscheme. In this case we may obtain more accurate estimate of inf M(v) for first loop execution.
In general case we can not obtain "last but one" loop execution condition. Instead of this we always have only "exit loop " condition. Thus we can not obtain in similary way more accurate estimate of sup M(v).
Now let's look how these considearions applyed to conventional case of sequential structured program.
Structured program consists of following basic constructions (other construcions can be builded from these):
Each of these basic constructions has representation by means of partly ordered sets. Namely:
sequence of operators can be represented as strictly ordered set
condition operator is represented as operation which produces different subset of output variables depending on sertain condition.
endless loop with exit-loop operator should be expanded and estimated as descrbed in Application to recursive program model.
Considered technicues allows to automatically determine positions for allocation/deallocation operators. It allows reduce number of errors linked with misspalcing of such kind of operators. And also allows developers to concentrate on other tasks but dynamic memory allocation.
Most significant lacks of considered approach are:
jan 20, 2001. last updated feb 22, 2001